Repost: Someone has to run the fabs
Egalitarianism is important but we neglect STEM education at our peril

In 2014, the city of San Francisco decided to try to improve equity in math education by barring kids from taking algebra in 8th grade. The results were highly disappointing — Black and Latino kids’ math skills did not improve, and the achievement gap widened, thanks to richer White and Asian families hiring private tutors to teach their kids algebra.
This incident — whose results are sad but entirely predictable — highlights how some Americans think we can increase equity in math education by simply teaching less math. But this doesn’t make the world more equal — rich kids have the private resources to learn on their own, while poor kids need the state to teach them. Paring back the role of the state is rarely a recipe for equity.
But there’s probably a wider consequence of this type of shenanigan as well. At a time when America is desperately trying to re-shore strategic industries like semiconductors, we need a broad workforce with basic numeracy even more than usual. The more we refuse to teach our kids math — not the well-prepared upper crust, but the broad middle of the distribution — the more we’ll be dependent on immigration to run the fabs. And while immigration is great, I don’t have infinite confidence in our government’s willingness to open the gates. We need to train our own people too.
Which means we need to get more serious about broad-based math education. A couple years ago, I wrote a post about why the fights over meritocracy vs. equity ignore the larger imperative of broad-based numeracy and technical competence. Here is that post, which I think is more relevant than ever.
A fab is a semiconductor fabrication plant — a factory where computer chips are made. They are huge, incredibly expensive things — a single fab can cost $17 billion, more than the entire 2020 capital expenditures of Facebook. Simply reading about what it’s like to work in a fab puts one in awe of modern technology. The amount of specialized machinery and software required to operate a fab is incomprehensible.
The amount of technical knowledge required to operate a fab is also staggering. When my friend, with a physics Master’s degree, went to work at an Intel fab, he found that he was the only person on his team without a PhD. A fab is a factory, but it’s not a 1908-vintage assembly line where people stand at an assembly line welding pieces of metal together to make a Model T. You have to understand advanced math and physics just to be able to make these machines run.
Which brings me to the point of this post. Fabs are a vivid illustration of the need for a strong STEM (science, technology, engineering, and mathematics) education system in the United States. In recent years there’s a push to de-emphasize STEM, mostly out of egalitarian concerns. But this push is wrongheaded. Egalitarianism is a worthy goal, but de-emphasizing or limiting STEM isn’t going to make us a more equal society; it’ll just make us economically weaker.
Our second Sputnik moment
A “Sputnik moment” is a historical reference to the launch of the first orbital satellite in October 1957. Though this was a triumph for humankind, it also triggered a panic in the United States, as we realized that the Soviet Union had a level of technical competence we hadn’t yet achieved (and which might be used for weapons). Sputnik made the U.S. wake up and realize the need for large-scale STEM education as a matter of national security. The response was the National Defense Education Act, whose provisions included, among other things:
financial assistance to public schools for STEM programs
funding for scholarships, graduate fellowships, and student loans
testing programs to identify talented students
funding for technical vocational training
Many believe that the NDEA was effective at making the U.S. one of the more scientifically and technically competent nations in the world. But it certainly shows the importance that the country’s leaders placed on STEM education.
Today, the U.S. is facing another kind of Sputnik moment — slower and less terrifying, perhaps, but no less crucial for our nation’s future. This is the shift of high-tech industries from North America to Asia.
U.S. prosperity depends on something called local multipliers. This means that stuff that we export brings in revenue from other countries, that then gets spread around the country via various service industries. In a 2010 paper, economist Enrico Moretti attempted to quantify this effect, and found the following:
[F]or each additional job in manufacturing in a given city, 1.6 jobs are created in the nontradable sector in the same city. As the number of workers and the equilibrium wage increase in a city, the demand for local goods and services increases. This effect is significantly larger for skilled jobs, because they command higher earnings. Adding one additional skilled job in the tradable sector generates 2.5 jobs in local goods and services. The corresponding figure for unskilled jobs is one. The multiplier also varies across industries. Industry-specific multipliers indicate that high tech industries have the largest multiplier. (Emphasis mine.)
What’s true for cities is true for countries as well. The U.S. economy benefits enormously from exporting things like Intel chips, Google software, Apple phone designs, Applied Materials chip-making machines, and so on. If these industries migrate to Asian countries, the U.S. will be less able to generate the wealth that local service industries and government redistribution spread around.
Biden seems to know this, which is why his economic program relies heavily on spending more on scientific research. Government-supported scientific discoveries trickle down to knowledge industries and preserve U.S. dominance of the kinds of high-tech activities that bring home the bacon so that the rest of our economy can spread the wealth around. This is what I call the “two-track economy”.
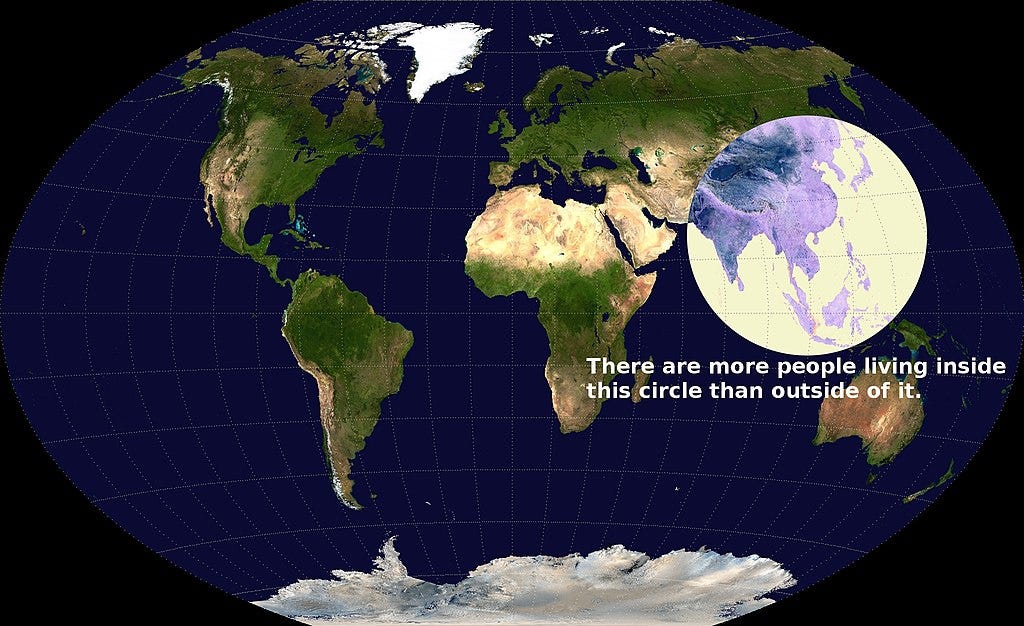
But U.S. dominance in these industries is always precarious, because the U.S. has far fewer people than Asia. Nothing illustrates this better than Valerie Pieris’ famous map:
This means that the U.S. market is destined to be smaller than the Asian market. We can ameliorate this disparity a bit by bringing in tons of immigrants, but the difference will always be large. Companies want to be close to their customers, so this means that in trying to keep industries like semiconductors, software, electronics and biotech in America, we’re swimming upstream against a vast global economic tide. This is even more true as China ramps up its industrial policy.
One crucial thing we need in order to keep knowledge industries on this continent is to have a large concentration of the world’s STEM talent. We do this in part through immigration, which is why skilled immigration is so crucial for our economic future (something Biden definitely realizes).
But due to the sheer numbers involved — and to the continual need to overcome stubborn resistance from nativists — immigration will only ever be a partial solution. In addition to the workers we get from overseas, we need to train a large and capable STEM workforce from our own population.
Thus, STEM education in the U.S. must be robust.
Currently, the U.S. produces plenty of math superstars (we regularly defeat China and Russia in the International Math Olympiad), but on broad measures of math education we don’t do so well. On international tests of reading ability, the U.S. scores well above the average for developed countries, but in math we score below average. We’ve improved a bit in recent years, but we’re still pretty mediocre.
That seems unlikely to produce the kind of broad-based technical workforce needed to staff the fabs and labs that power U.S. knowledge-based industries. Of course, most workers in those industries will occupy a mezzanine level of STEM skill between “star researcher” and “able to pass a high school math test”. But the fact that such a high percentage of our grad students in STEM fields are from overseas suggests that there’s huge room for improvement in how well we train our own workers.
But what does it take to make STEM education more robust? That’s a harder question.
Learning vs. screening
At a dinner during my freshman orientation in college, I sat next to a physicist who would eventually become my freshman advisor. During the dinner he leaned over to me and said “Sometimes, I think all I do is screen.”
He was the best teacher I had in all of college. I felt that his ability to make learning physics interesting, and convey concepts at a deep level, did a lot for me personally. So I’m pretty sure he was wrong, and teachers — especially him — do a lot more than screening.
But I do worry that STEM education in the U.S. is excessively focused on screening. The original NDEA placed great emphasis on identifying and supporting gifted and talented students. This idea persists to the present day, where placement into advanced STEM courses is often done based on test scores or subjective teacher identification. In fact, the idea that STEM talent is inborn and education is mostly for the purposes of screening (or “signaling”) is commonplace, and I believe that it’s far more pervasive among educators than they would publicly let on.
In 2013, my PhD advisor Miles Kimball and I co-authored an op-ed arguing that the focus on natural talent in American math education is wrongheaded. We wrote that a pervasive belief that math ability is inborn hurts both kids who do well in math classes (who become complacent) and kids who do poorly (who become discouraged).
Again and again, we have seen the following pattern repeat itself:
Different kids with different levels of preparation come into a math class. Some of these kids have parents who have drilled them on math from a young age, while others never had that kind of parental input.
On the first few tests, the well-prepared kids get perfect scores, while the unprepared kids get only what they could figure out by winging it—maybe 80 or 85%, a solid B.
The unprepared kids, not realizing that the top scorers were well-prepared, assume that genetic ability was what determined the performance differences. Deciding that they “just aren’t math people,” they don’t try hard in future classes, and fall further behind.
The well-prepared kids, not realizing that the B students were simply unprepared, assume that they are “math people,” and work hard in the future, cementing their advantage.
Thus, people’s belief that math ability can’t change becomes a self-fulfilling prophecy.
We wrote that the U.S. should focus less on identifying talent and more on promoting work ethic and perseverance.
One thing we talked less about, but which I believe strongly in, is the importance of long-term motivation. It’s easy enough to motivate youngsters with parental and teacher pressure, but once they enter the long slog of adult life, they’re only going to work in a fab if they want to. At least two people I went to high school with are now mathematicians despite not being among the top scorers on childhood tests (meanwhile, I write op-eds for a living!). And while some child prodigies eventually become STEM stars, but some insist on having normal, average lives and careers. In other words, what people want to do is ultimately more important than what they’re told to do.
And both work ethic and personal motivation matter when on the job. TSMC, the Taiwanese semiconductor manufacturer who has been grabbing headlines by pulling well ahead of Intel in the technology race, is famous for its corporate work ethic and esprit de corps.
So in order to excel in the crucially important knowledge industries — in order to have a workforce that can run the fabs — I think we should focus our education system less on screening and more on hard work, motivation, and education that actually improves learning.
Unfortunately, much of our education policy conversation seems to be trapped in a toxic debate over excellence vs. equity.
STEM education vs. equity?
The other day, there was some controversy about a plan by the Virginia Department of Education that, according to some reports, prevent students from taking accelerated math courses until the 11th grade. Equity was given as one reason for this change. The details of the program aren’t completely clear yet, but a Twitter discussion revealed that many people are indeed concerned that accelerated STEM education creates inequity.
To supporters of the move, allowing students to take accelerated classes inherently represents “tracking”. Sure, you can call the courses electives and allow students to choose whether they take normal or accelerated courses, but since math is cumulative — earlier subjects are prerequisites for later ones — the kids who take advanced courses earlier will be better prepared for advanced classes later. Hence, they will be on a different “track”, whether it’s compulsory or not.
To detractors, meanwhile, the move was indicative of a slide toward the kind of dystopia described in Kurt Vonnegut’s short story “Harrison Bergeron”, where natural differences in beauty, intelligence, and athletic ability are cancelled out by “handicap” technologies that the government forces everyone to wear. To these critics, forcing students into easier math classes than they can handle is simply a way of forcing handicaps on those with inborn talent.
This debate will come as no surprise to anyone who even casually follows American education policy. “Gifted and talented” programs are a constant flashpoint for controvery; just recently, after a bitter and protracted debate that broke down over similar lines, New York City decided to replace its admissions for gifted and talented programs with a combination of teacher recommendations and a random lottery.
The problem with this debate is that both sides are misguided. The opponents of gifted education are generally focused on the wrong kinds of equity, while the supporters of gifted education are generally too focused on education as talent screening.
People who think that gifted education, accelerated math classes, etc. are engines of inequity are only partially right. Yes, it’s possible for selective schools to become pipelines to success that leave others behind, but plenty of research and many policy experiments have shown that school choice is not very effective at improving grades. And the practice of shunting kids into accelerated math classes based on test scores hasn’t been shown to have a long-lasting effect (though interestingly it does seem to modestly decrease racial and gender gaps in access to accelerated classes).
Forcing kids to take all the same classes is just focusing on the wrong kind of equity. What ultimately matters are economic outcomes, and those can (and should) be made more equitable through taxes, spending, and other economy-wide measures. We shouldn’t stop kids from taking hard STEM classes just because we’re worried that they’ll have a better chance of becoming rich STEMlords; instead, we should just tax the STEMlords more (in fact, the STEMlords themselves tend to support this). In fact, we don’t need an economically unequal society in order to incentivize people to run the fabs — those TSMC engineers working dawn to dusk aren’t even making big bucks.
In fact, even within the academic system, accelerated classes don’t have to (and shouldn’t) create inequity. I took advanced math and physics classes in college, and there were plenty of humanities kids who got higher GPAs than I did. Yes, there’s the annoying practice of giving extra GPA points for honors classes, and that should be abolished. But if you abolish that, then taking accelerated classes will actually tend to make kids get lower GPAs; they’ll only do it if they’re motivated to learn.
Supporters of gifted education, meanwhile, all too often focus on talent screening rather than effective education. The disappointing long-term results of shunting kids into accelerated classes based on test scores suggest that motivation ultimately matters more than ability. But even more fundamentally, the notion that the purpose of education should be to discover and elevate natural talent is fundamentally flawed, as the entire previous section of this post argued. Finding a few kids capable of defeating China in a math competition is useless compared to the task of training millions of kids to work in high-tech export industries.
So while U.S. STEM education languishes, the debate over how to improve it seems locked in a pointless struggle over whether or not to enforce equity along unimportant dimensions or go hunting for natural talent to celebrate and reward. In fact, neither of these things should be the focus of a good STEM education system. We should be laser-focused on the question of how to educate and motivate a broad-based skilled workforce capable of sustaining the knowledge industries that are America’s main hope for continued economic relevance in the world, and how to structure the rest of our economic system to equitably redistribute the prosperity those industries create.
I don’t pretend to have all the answers for how to do that; at best, I have a few ideas and guesses. Building a system to produce broad-based high-level STEM competency is a huge task; such a system will require decades of dedication and millions of people to put it into place. What I insist that we do is to refocus our STEM education debates on the right question. And that question is not “Who deserves what"?”. It’s “Who will run the fabs?”.


I mostly agree with your points, but in practice my experience teaching mathematics is that often by *trying* to teach more kids math we make sure only the gifted really understand it. The problem is the incentives favor moving more to rote learning when you try to get more students to succeed and the end result is often only the very gifted actually can extract real conceptual understanding from the class.
The problem is that even if you're intelligent and conscientiousness if you hate math and thinking about it makes you feel frustrated and miserable it's exceptionally difficult to engage in the kind of hypothesis generation and testing (ohh maybe it works like this) needed to get a real conceptual understanding. If the teacher asks questions that can't be done by rote and test real conceptual understanding those students just can't do them.
OTOH those students can memorize rote rules with enough effort and pain. The net result is that the incentives for the school, teachers and most students are to just learn those rote rules. The very gifted students can still extract understanding but you've lost all the kids in the middle who could have excelled in a class that asked conceptual questions on exams and required real understanding. But I fear that in order to reach those students your incentives have to allow for the fact that you can't give a backup rote mechanism for doing well (so some motivated students ..even with pushy parents.. won't succeed).
So I sorta agree with you in principle but I fear that when you give this as a policy goal the way it trickles down into the classroom is to incentivize teachers to increase the fraction of students who succeed in meeting some testing threshold and that often means presenting the class with a list of rote tricks. So instead of getting say (in say a high achieving suburban class) 70% of kids who leave with real understanding you get 20% with real understanding and 90% who can manage to the computations (and forget them once the class ends).
I think this perspective, combined with the research around deliberate practice, does result in policy recommendations that will have a lot of enemies. Far more hours of the school day need to be used for guided practicing of math.
The way more people learn math is to have more time doing exercises in a deliberate practice framework (eg JUMP math is one example, khan academy another). But homework is a bad tool for this because real time correction and redirection is essential. The goal is to be practicing at the edge of ability, which means it’s easy to get blocked without a guide.
This does mean less time for other topics. From my perspective, there does not need to be as much time spent on study that is mostly memorizing names and facts.
But I expect this recommendation to provoke a lot of disagreement.