Contemplating a world of linear growth

Plus: Some fun econ papers!

I’m in the mood to write about some econ papers today.

The most interesting one I’ve come across recently is Thomas Philippon’s working paper on “additive growth”. Back in April, he wrote a Twitter thread explaining the paper’s basic findings and arguments:

Thomas PHILIPPON @ThomasPHI2

(1) New Working Paper: the fundamental driver of growth in modern economies, Total Factor Productivity (TFP), is linear, not exponential. This is a paper I did not expect to write...

So, let me unpack this a bit for those who aren’t well-versed in the concepts already. Total Factor Productivity is the part of GDP that we can’t explain in terms of inputs like labor, capital, and land. An economist once called it “a measure of our ignorance”. And yet in the long term, TFP is the most important driver of growth in living standards, because we know we can max out all the other stuff. Once you put all the people to work and build all the buildings and machines and roads you need, you can only keep growing by using those inputs in a smarter way. That’s TFP.

Many people identify TFP with technology, which is obviously an important piece of it, but the two aren’t quite the same. In fact, we don’t know exactly what TFP is — we only know we want more of it.

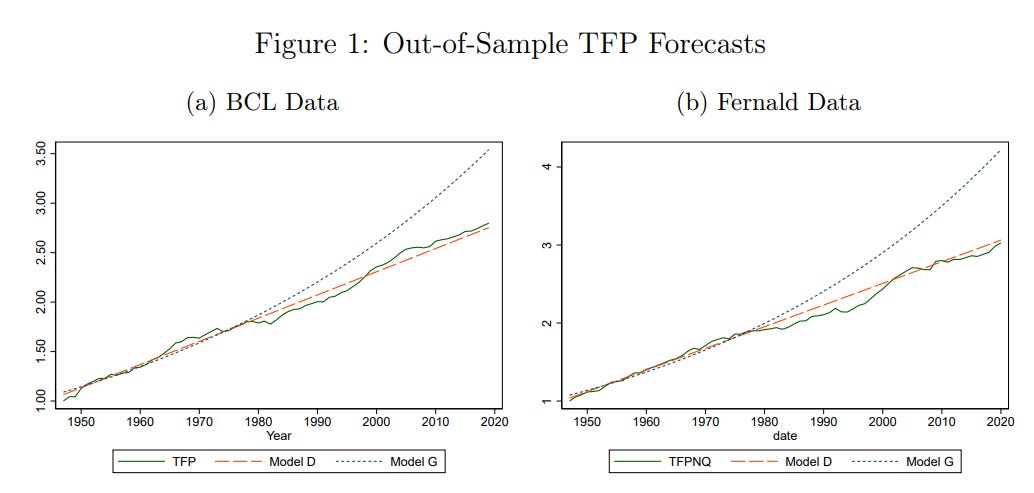
Most economic models assume that TFP grows exponentially. The reason is partly that GDP itself often looks like it grows exponentially, but this assumption is also easy to work with mathematically (Never underestimate economists’ ability to convince themselves that the world works in a way that’s convenient for their equations!). But TFP might not grow exponentially. It might grow linearly — or “additively”, as Philippon puts it. TFP might be a straight upward line instead of curve that explodes upward faster and faster. Philippon plots two different measures of U.S. TFP growth since WW2, and finds that they look more like a straight line than an exponential curve:

The rest of the paper is basically just Philippon doing a bunch of checks to show you that no, your eyes aren’t tricking you, it really is just a straight line.

Economists have definitely noticed that the percentage growth rate of TFP has been slowing down in recent decades — it slowed in the 70s and 80s, accelerated again in the 90s and early 00s, then slowed back down. (Exponential curves have a constant percentage growth rate.) But they still maintained the belief that whatever underlying process drives growth was fundamentally exponential, and that the rate of exponential growth was simply falling. Now here comes Philippon and says no, it’s just that it was always a straight line all along.

Ahh, but was it a line all along? As many other observers have already noted, when Philippon extends the line back before WW2 for the U.S. and the UK, he finds that the slope of the line changed, probably multiple times:

Philippon’s explanation for this is that growth is normally linear, but that it shifts each time a new general-purpose technology such as electrification or steam power arrives on the scene. (Yes, this is why Google OpenAI punningly named their machine-learning language model “GPT-3”; they are hoping that machine learning is the new big paradigm.) Each new GPT, Philippon says, enables faster linear growth going forward.

So really the two models we’re looking at are not “exponential curve” vs. “straight line”. They’re “exponential curve that has recently slowed down because we’re discovering fewer new technologies” vs. “straight line that keeps getting faster each time a big new technology is discovered”. To be honest, I’m not sure those two models tell us such very different things about our world. In the first case, we can expect linear growth at about the current pace unless we discover another GPT. In the second case, we can expect exponential growth at a slower percentage rate than before unless we accelerate the pace of technological innovation. In both cases, the message is clear: Discover more useful technologies, or living standards won’t rise as much. Well, OK then. Let’s discover some awesome new technologies!

(By the way, I often say that macroeconomics is hard because we “don’t have enough data”. Well, this is exactly what I’m talking about. Even 4 centuries of data isn’t enough to tell us whether growth is linear or exponential!)

There’s also the question of why we would expect TFP growth to have any kind of long-term functional form in the first place. Why would it be either consistently linear or consistently exponential?

Exponential growth processes are typically things where “like begets like”. Population growth, for example, is exponential (in the absence of limiting factors), because people give rise to other people. It makes sense that per capita GDP growth would have an exponential component, because you use capital to build more capital. And indeed, as Dietz Vollrath has noted, U.S. GDP growth since WW2 does look a lot more exponential than TFP growth does.

But why would TFP work this way? Lots of economists have made various models to try to explain why TFP might be exponential — these usually involve combinatorial innovation, i.e. producing new ideas using old ideas. That makes conceptual sense — for example, you need to know how both electric current and semiconductors work in order to build a transistor. But there’s no real way to quantify or measure these ideas — all we can really measure is TFP itself. The “stock of ideas” is kind of this fantasy variable we think about in the background. So whether ideas “give birth” to other ideas at some constant rate is not something we’ll ever know.

And as Vollrath points out, the relationship between this imaginary “stock of ideas” and TFP itself could change over time. Even if ideas give birth to new ideas at a constant rate, each idea might increase TFP less than the one before it (maybe because we went for the most useful ideas first). Vollrath shows that if you assume that TFP is equal to the natural log of the number of ideas, and if ideas give birth to each other at a constant rate, you get perfectly linear growth. Cool result! But again, unless we someday figure out a way to measure the amount of “ideas” directly, all this is just sort of blowing smoke.

I think the really interesting thing about Philippon’s paper is that it forces us to think about what a world of linear growth would be like in the future. A world of linear growth would not be a world of stagnation — things would keep getting steadily better and better. But it would also not be the kind of explosively better utopia that many economists posit.

For one thing, linear growth would mean that silly physicists could no longer barge into econ discussions and bellow that exponential growth can’t continue forever because in a few thousand years we would use all the energy in the Universe and blah blah blah. Linear growth means that the Universe would have plenty of room for us to grow for a very long time.

But it’s not clear that linear growth would be good for the environment. Remember, degrowth is fundamentally wrong, because a lot of economic growth involves innovating ways to produce more utility from fewer resources. Linear TFP growth would slow down the rate at which we innovate, and thus might slow down the rate of the green innovation that we need to make modern economies sustainable.

In terms of policy objectives, linear growth would give us more of a reason to care about the present day. In his book Stubborn Attachments, Tyler Cowen argues that since the effects of growth compound so strongly over time, we should prioritize growth over practically everything else in the short term. That’s a reasonable argument. But if growth is only linear rather than exponential, the argument becomes a bit less powerful — yes, we still need to care a lot about keeping up growth rates, but we then have more room to care about other stuff in the present, like inequality.

The most interesting question, I think, is whether people would be happy in a world of linear growth. If people tend to judge their situation by comparing themselves to their parents, then linear growth should still satisfy them, because — barring negative shocks — everything still keeps getting better and better.

But in percentage terms, the improvement would get smaller and smaller every decade. Going from making $10,000 a year to making $60,000 a year is a lot more of a psychological and emotional boost than going from making $500,000 to making $550,000. Since humans have diminishing marginal utility of consumption, they might need exponential growth just to preserve that feeling of “OMG my life is so much richer and easier than before”. So that giddy, heady feeling of rapid growth might be confined to the early stages of industrialization. That could conceivably lead to boredom, or to people seeing the world as more of a zero-sum competition.

Then again, the early stages of industrialization were a very chaotic time. We had world wars, the rise of communism and fascism, and sweeping disruptive social changes. A world of linear growth might avoid such ructions in the future, by giving us more time to react to each percentage change in the world around us.

Personally, I’m not so afraid of a linear growth world. A world that gets better at a stately, measured pace is not as fun as one where everything just explodes into galactic utopia. But it’s a heck of a lot better than stagnation, or a boom and crash. In fact, Noahpinion has been experiencing linear subscriber growth since its inception, and I’m pretty happy with that.

Anyway, now for a couple of bonus econ papers.

Why we got inflation this time

Ricardo Reis is one of my favorite macroeconomists, always looking at the big picture, thinking outside the box, and looking for just the right data. In a new paper, he analyzes why the current bout of inflation happened. There are some slides here.

Reis’ story starts with the obvious stuff — a fast recovery, a bunch of supply chain snarls related to the pandemic, higher energy prices from the Ukraine war, and a Fed that was too slow to see the inflationary danger emerging in 2021. Later in the paper he goes into some technical reasons why he thinks the Fed was too dovish.

But then the story gets interesting. Reis argues — based on his earlier research — that after the Great Recession, people gradually stopped believing that the Fed would really stick to its 2% inflation target. At first, this meant that expectations got “de-anchored” in the downward direction — people decided that 2% was the ceiling instead of the actual target. But when inflationary pressures spiked in 2021, expectations flipped, and became de-anchored on the high side. Of course, inflation expectations can become a self-fulfilling prophecy — if businesses decide prices are going to go up, they raise their prices preemptively — so this made inflation take on a life of its own.

To be perfectly honest, I’m a bit skeptical of this part of Reis’ story. His main measure of inflation expectations comes from household surveys, but to me, market expectations of inflation are a better measure, because A) they come from professionals who are probably more similar to the businesspeople who actually set prices, and B) they require people to bet on their beliefs instead of simply expressing generalized anxiety about the state of the world.

So when we look at market expectations, what do we see? 5-year inflation expectations spiked up to about 3.5% but have since come most of the way back down, while expectations for 5 to 10 years from now never really budged much and stayed lower than they were in the early 2010s.

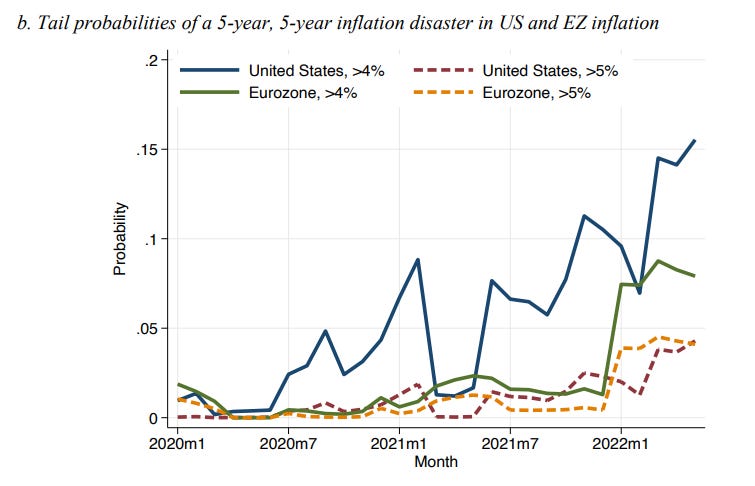
Reis has a stronger argument, I think, when he talks about the distribution of expectations. Markets’ pegged the likely scenario as just a small, short-term rise in inflation. But at the same time, they thought the risk of high and persistent inflation increased. Here is Reis’ graph:

In other words, by early 2022, markets didn’t think that a 10-year-long bout of 4-5% inflation was the likeliest outcome, but they no longer thought it was out of the realm of possibility. That might have pushed up actual inflation, as companies raised their prices to hedge their bets. And it emphasizes the importance of Fed credibility — in other words, this is an argument that even if inflation expectations stay moderate, the Fed should raise rates aggressively to make sure everyone knows it’s still willing to do whatever it takes to quell inflation.

The end of the tax cut rainbow

By the time George W. Bush did his big tax cuts in 2001 and 2003, it was clear to most economists that we had reached the logical end of that policy — that slashing personal income taxes was no longer going to boost the economy the way it might have done in the early 60s when John F. Kennedy did it. But many economists and pundits — including myself — held out hope that corporate tax cuts could still boost investment and growth. Corporate tax cuts should get more bang for the buck, because theory says that business investment (which corporate tax applies to) is easier to disrupt and distort than personal consumption and savings.

So Trump cut corporate taxes in late 2017, and many of us were optimistic about the effects. But although the economy did grow robustly in the two years that followed, there was some evidence that the corporate tax cuts didn’t really do a lot. The late Alan Krueger sent me some data he collected with David Cho, showing that industries that benefitted proportionally more from Trump’s corporate tax cuts didn’t hire more people than other industries in 2018. Oh well. This is probably one reason the Democrats felt safe hiking corporate taxes in the recent Inflation Reduction Act.

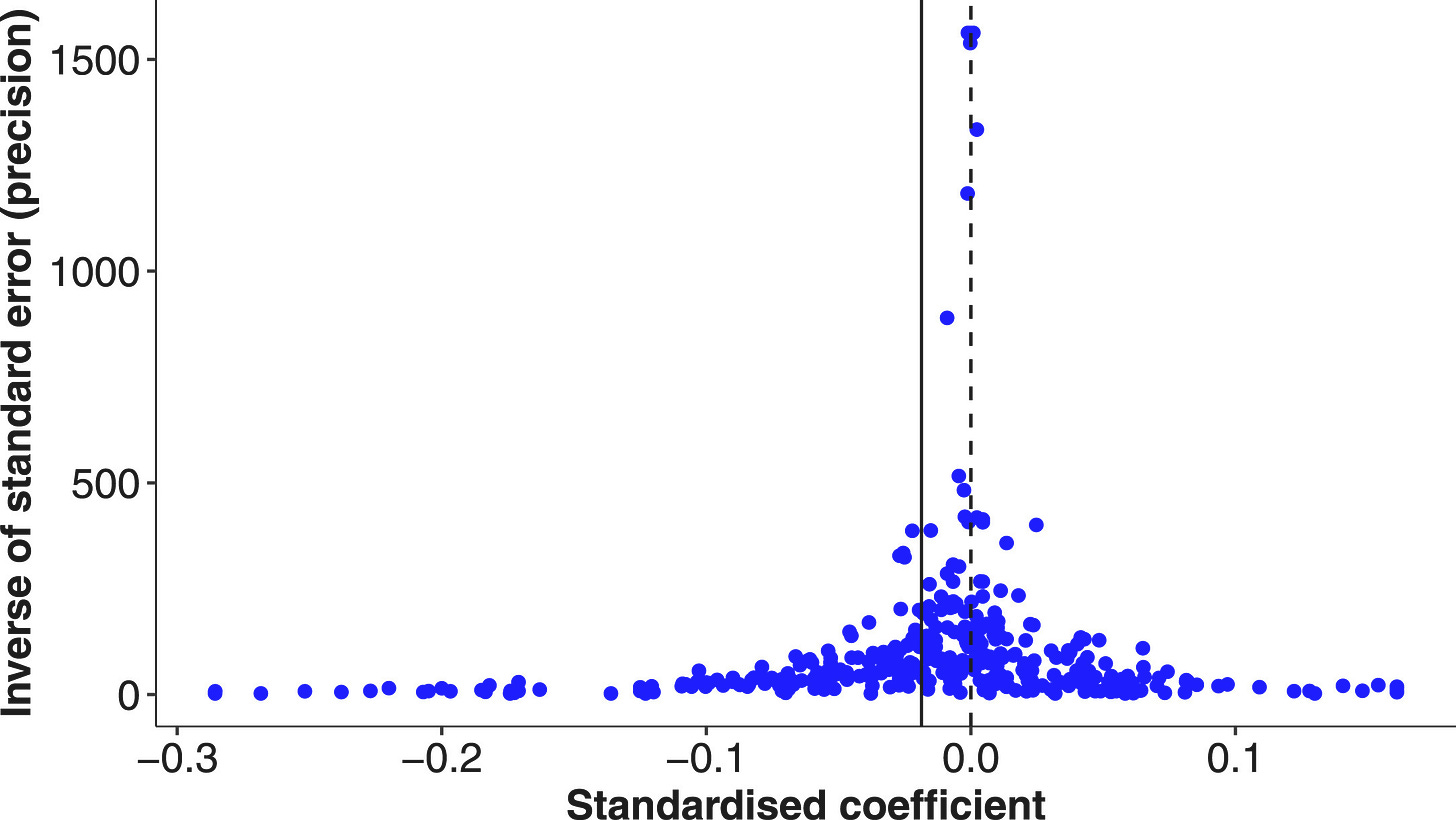
Now, a paper by Gechert & Heimberger says that I probably shouldn’t have been so optimistic in the first place. There are a number of studies that do find modest benefits from cutting corporate taxes. But Gechert & Heimberger say that this was simply an artifact of publication bias. If empirical estimates of the effect of corporate tax cuts were being fully reported, the estimates should be roughly symmetric around the true value. But instead they’re asymmetric; the distribution leans toward finding that higher corporate taxes are bad:

Basically, corporate tax cuts haven’t really done much for countries around the world in recent decades. That doesn’t mean that any level of corporate taxation is fine — if you taxed companies at, say, 99%, they’d all just go off the books or close down. But what it means is that current levels of corporate taxes probably aren’t high enough to be a major drag on business activity.

Which means that we’ve sort of come to the end of the tax cut rainbow that started in 1963. We cut personal taxes until it was clear there was no more benefit to cutting them more, and then we did the same with corporate taxes. Whatever policies we rely on to boost growth in the future, tax cuts won’t be a major arrow in our quiver.

---